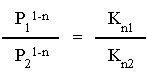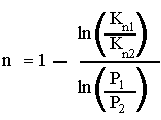Single Burn Propellant CharacterizationJames E. Lanier My book "Designing Rocket Motors" showed a way to measure "a" and "n" using c* burners with 2 example burns. We really only need burn rate "r" at a single known value of pressure and 2 pressure readings at 2 known values of Kn. ( c* or Isp* are fairly flat with pressure)
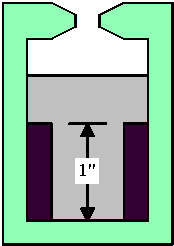
This diagram shows a c* burner with a burning surface that changes in area. When the propellant is first ignited the pressure will slope upwards from zero to its final stagnation pressure that is associated with the Kn (of the larger surface area). We are unconcerned with the burn rate here but just the pressure after the initial transition. The pressure will suddenly drop to a lower value associated with the smaller area and Kn. We will calculate this burn rate and record this value of pressure. from eq 6 we know that: P = Kn Isp* rwt r note: see foot note for explanation of Isp* and r = a Pn so P = Kn Isp* rwt a Pn or P(1-n) = Kn Isp* rwt a Since we have 2 values, then P1(1-n) = Kn1 Isp* rwt a and P2(1-n) = Kn2 Isp* rwt a so
and solving for n we have
We know the burning rate at P2 so we can now find "a" from r = a P2n so that a = r / (P2n) That's it! Basically, we have eliminated the need for detection wires in the grain by already having a good solid steady burn before we start measuring rate. It is now very easy to determine the value of Isp* since Isp* = P2(1-n) / (Kn2 rwt a) and rwt has been directly measured and calculated. notes: Isp* is a parameter derived in "Designing Rocket Motors". It is equal to (c*/g). rwt is propellant weight density in pounds per cubic inch. Important! This article is an exercise describing a mathematical basis for propellant characterization. Actual characterization test burns can be very dangerous. A great deal of knowledge and expertise are required for such endeavors. No attempt is made here to show anything beyond a mathematical model for such tests. |
|
|
|
|